This is an example of a fractal, generated recursively. We use simple plot commands, holding the current graphics.
>A=[cos(pi/3),-sin(pi/3);sin(pi/3),cos(pi/3)]; >B=inv(A); >function koch (x,v,n) ...
global A,B;
if n==0 then
hold on;
plot([x[1],x[1]+v[1]],[x[2],x[2]+v[2]]);
hold off;
else
w=v/3;
koch(x,w,n-1); x=x+w;
w1=A.w; koch(x,w1,n-1); x=x+w1;
w1=B.w; koch(x,w1,n-1); x=x+w1;
koch(x,w,n-1);
endif;
endfunction
One level deep, the Curve looks like this.
>plot2d(none,a=0,b=1,c=0,d=1); ... koch([0;0],[1;1],2):
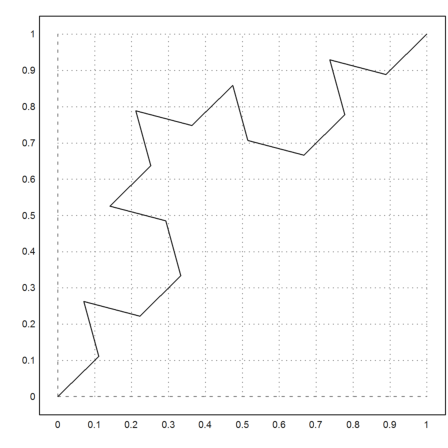
Several levels deep, we relace every straight line with one curve of the same shape over and over again.
The work grows exponentially. n=7 is about the most, Euler can do.
>plot2d(none,a=0,b=1,c=0,d=1); ... koch([0;0],[1;1],7):
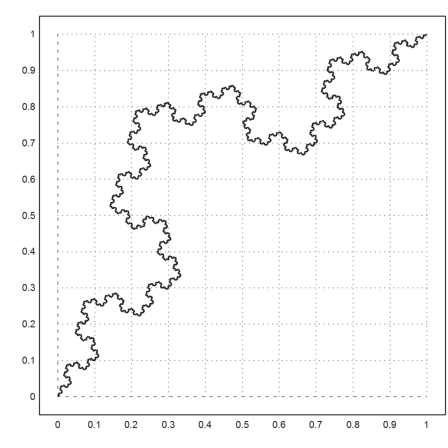
In fact, the generation of a fractal is much faster in Python. Moreover, Python has growing lists. Euler has such lists too, but you would need to import a C library for this.
But notice that the plotting takes the most time whatever you do.
>function python ...
import math;
x,y = 0,0
vx=[x]
vy=[y]
def fd (delta,alpha):
global x,y,vx,vy
x=x+delta*math.cos(alpha*math.pi/180)
y=y+delta*math.sin(alpha*math.pi/180)
vx.append(x)
vy.append(y)
def dragonrek (delta,alpha,n,left):
if n==0:
fd(delta,alpha)
else:
signum=2*left-1
dragonrek(delta/math.sqrt(2),alpha+signum*45,n-1,False)
dragonrek(delta/math.sqrt(2),alpha-signum*45,n-1,True)
def dragon (n):
global x,y,vx,vy;
x,y=-1,0
vx=[x]
vy=[y]
dragonrek(2.0,0,n,False)
return [vx,vy]
endfunction
>v=py$dragon(12); ... fullwindow(); ... plot2d(v[1],v[2],a=-1.7,b=1.5,c=-2,d=1.2,grid=0):

Let us take the challenge in Euler. We need global values as in Python for an efficient implementation. Expanding and returning an Euler vector in each call to fd would be very slow. And we do not want to use Euler's global lists.
>function fd (delta, alpha) ... global x,y,V,Vn x=x+delta*cos(rad(alpha)); y=y+delta*sin(rad(alpha)); Vn=Vn+1; V[1,Vn]=x; V[2,Vn]=y; endfunction
These functions are very similar to the Python implementation.
>function dragonrek (delta,alpha,n,signum) ...
if n==0 then fd(delta,alpha);
else
dragonrek(delta/sqrt(2),alpha+signum*45,n-1,-1);
dragonrek(delta/sqrt(2),alpha-signum*45,n-1,1);
endif;
endfunction
Now we define the global variables, setting V large enough.
>x=-1; y=0; n=12; V=zeros(2,2^(n+1)); Vn=1; V[1,1]=x; V[2,1]=y; ... tic; dragonrek(2,0,n,-1); toc;
Used 0.102 seconds
I told you, that Python would be faster.
>tic; py$dragon(n); toc;
Used 0.008 seconds
But the plot takes most of the time.
>tic; plot2d(V[1,1:Vn],V[2,1:Vn],a=-1.7,b=1.5,c=-2,d=1.2,grid=0); toc;
Used 0.55 seconds